Примеры записи команд:
7LQ2 - В любом случае записываем в ячейку число - 7, далее двигаем каретку на один шаг влево (команда L) и переходим в состояние - Q2
]HQ1 - стираем ячейку, делаем ее пустой, даже если она и была пустой - ], стоим на месте (команда H) и переходим в состояние (столбец)- Q1
xHQ0 - записываем в ячейку букву - x, стоим на месте (команда H) и остонавливаем выполнение программы - Q0
Машина Тьюринга, примеры решения задач:
задача1.
Увеличить число на единицу, записанное в двоичной системе счисления.
- Каретка находится слева от числа (до числа)
- Каретка находится над числом
Решение:
Для решения данной задачи нам необходимо определить множество всех значений алфавита, так как речь идет о двоичной системе счисления, то в поле “ алфавит ” запишем числа 0 и 1. Программа автоматически добавит в столбец слева от таблицы "программа" введенные числа и знак пустой ячейки - ]. В задаче не сказано, к какому именно числу необходимо добавить единицу, а значит, берем произвольное двоичное число и записываем его в поле «слово».
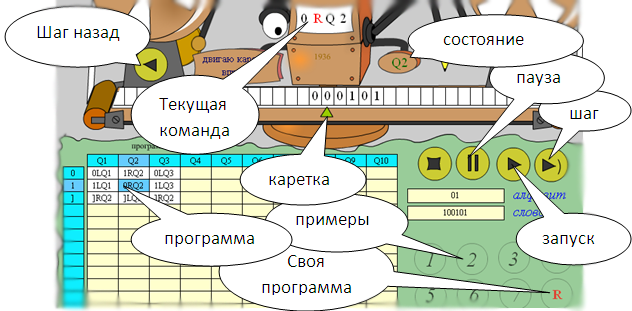
Далее самое интересное – кодирование. Из условия задачи для пункта «а» сказано, что каретка находится слева от слова, это значит что само слово нужно еще и найти. Сам автомат (каретка) кроме текущей ячейки ничего не видет, он может только прочитать ее содержимое и на основании значения, которое он считывает, безусловно выполняет поручения. А видит он пустую ячейку. Даем команду двигать в право до тех пор, пока он не увидит начало слова - команда ]RQ1. С точки зрения автомата:
если ячейка пуста
- нахожусь в состоянии Q1
- считываю значения текущей ячейки
- если она пуста то записываю в нее пустоту (звучит странно но так оно и есть, хотя я всеже добавил здравый смысл в свой эмулятор и он просто пропускает такой шаг)
- двигаю каретку вправо на один шаг
- перехожу (даже если я и находился там) в состояние Q1
если ячейка содержит значения 0 или 1 выполняем команды 0RQ2 и 1RQ2
C точки зрения автомата:
- нахожусь в состоянии Q1
- считываю значения текущей ячейки
- если это 0 или 1 то продолжаю двигаться вправо и перехожу в состояние Q2
Автомат переходит в состояние Q2 (второй столбец), так как функция состояния Q1 - найти число находящегося на ленте, выполнена. Число на ленте найдено. Каретка теперь находится над числом и теперь необходимо найти его конец, для продолжения выполнения программы. Для этого продолжаем двигать каретку вправо, до тех пор, пока не наткнемся на пустую ячейку (означает конец числа на ленте) - команда ]LQ3, при выполнении которой автомат переходит в сотояние Q3.
| Q1 | Q2 | Q3 | |
| 0 | 0RQ2 | 0RQ2 | 1HQ0 |
| 1 | 1RQ2 | 1RQ2 | 0LQ3 |
| ] | ]RQ1 | ]LQ3 | 1HQ0 |
Из таблицы видно, что автомат в состоянии Q3 выполняет арифметические действия над вводимым числом. Алгоритм для двоичного числа очень прост, считываем, и если это ноль, то заменим значение ячейки единицей и останавливаем программу, если единица, то меняем на ноль и переходим на шаг влево, где алгоритм повторяется для текущей ячейки, и так далее.
Задача 2.
Напишите программу для машины Тьюринга, которая проверяет любое введенное десятичное число на четность.
Решение:
- Алфавит - множество всех цифр от 0 до 9 и вывод результата «Y» (да), «N» (нет)
- Слово - любое десятичное введенное число
- Каретка находится над словом (для простоты)
| Q1 | Q2 | Q3 | Q4 | |
| 0 | 0RQ1 | 0RQ3 | ||
| 1 | 1RQ1 | 1RQ4 | ||
| 2 | 2RQ1 | 2RQ3 | ||
| 3 | 3RQ1 | 3RQ4 | ||
| 4 | 4RQ1 | 4RQ3 | ||
| 5 | 5RQ1 | 5RQ4 | ||
| 6 | 6RQ1 | 6RQ3 | ||
| 7 | 7RQ1 | 7RQ4 | ||
| 8 | 8RQ1 | 8RQ3 | ||
| 9 | 9RQ1 | 9RQ4 | ||
| Y | ||||
| N | ||||
| ] | ]RQ2 | YHQ0 | NHQ0 |
С точки зрения автомата:
- нахожусь в состоянии - Q1
- если это цифра, то двигаю каретку на шаг вправо и перехожу в состояние - Q1
- если это пустая ячейка, то двигаю каретку на шаг влево и перехожу в состояние - Q2
- если эта цифра 0,2,4,6,8 - двигаю каретку на шаг вправо и перехожу в состояние - Q3
- в состоянии Q3 стою на месте, записываю букву Y и останавливаю программу - Q0
- если эта цифра 1,3,5,7,9 - двигаю каретку на шаг вправо и перехожу в состояние - Q4
- в состоянии Q4 стою на месте, записываю букву N и останавливаю программу - Q0
От автора:
Данная программа эмулятора была задумана лишь для изучения простейших алгоритмов. Сложные программы писать по Тьюрингу пустая трата времени.